3. Convert Infix Expression to Prefix Expression
Problem:
Given an infix expression, output the expression in Prefix (Polish Notation) form.
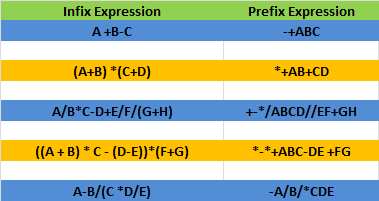
For e.g.
Solution:
This implementation is done using C#.NET.
ALGORITHM:
This algorithm maintains two stacks. 1st stack for all operators and 2nd stack to store the operands.
1) Validate the Infix Expression for correctness
a) ‘(‘ and ‘)’ are in pairs
b) Operator is in between 2 operands (Binary operators are considered only)
2) If Infix Expression is Valid then
a) Push ‘(‘ to Operator Stack and Append ‘)’ to Infix Expression
b) Scan each character in the Infix expression
i) If scanned character is ‘(‘
Then
Push it to Operator Stack
ii) Else If scanned character is ‘)’
Then
(a) Repeat the below steps until ‘(‘ is popped out from Operator Stack
(b) Pop from Operator Stack into OPERATOR
(c) If OPERATOR != ‘(‘
(i) Pop twice from Operand Stack into OPERAND2 and OPERAND1
(ii) Push “OPERATOR OPERAND1 OPERAND2” in Operand Stack
iii) Else If scanned character is an Operator
Then
(a) Repeat the below steps until Operator having low precedence than Scanned character is popped out from Operator Stack
(b) Pop from Operator Stack into OPERATOR
(c) If OPERATOR has Higher or Equal Precedence than scanned character
(i) Pop twice from Operand Stack into OPERAND2 and OPERAND1
(ii) Push “OPERATOR OPERAND1 OPERAND2” in Operand Stack
(d) Otherwise,
(i) Push the last Popped operator back in Operator Stack
(ii) Push the scanned character in Operator Stack
iv) Otherwise, Scanned character is an operand. Thus, Push it in Operand Stack
c) Pop from Operand Stack which is the final expression and return;
public void ConvertInfixToPrefix(string infixExpression)
{
try
{
ValidateInfixExpression(ref infixExpression);
}
catch (Exception ex)
{
Console.WriteLine(“Invalid infix expression. Error Details:{0}”, ex.Message);
return null;
}
Stack operatorStack = new Stack();
Stack operandStack = new Stack();
operatorStack.Push(‘(‘);
infixExpression += ‘)’;
foreach (char ch in infixExpression)
{
if (ch == ‘(‘)
{
operatorStack.Push(ch);
}
else if (ch == ‘)’)
{
// Pop from operator Stack until ‘(‘ is encountered
char poppedOperator = operatorStack.Pop();
while (poppedOperator != ‘(‘)
{
operandStack.Push(PrefixExpressionBuilder(operandStack, poppedOperator));
poppedOperator = operatorStack.Pop();
}
}
else if (IsOperator(ch))
{
// Pop all operators from Operator Stack which have same or higher precedence
char poppedOperator = operatorStack.Pop();
bool sameOrHighPrecedence = CheckSameOrHighPrecedence(poppedOperator, ch);
while (sameOrHighPrecedence)
{
operandStack.Push(PrefixExpressionBuilder(operandStack, poppedOperator));
poppedOperator = operatorStack.Pop();
sameOrHighPrecedence = CheckSameOrHighPrecedence(poppedOperator, ch);
}
operatorStack.Push(poppedOperator);
operatorStack.Push(ch);
}
else
{
operandStack.Push(ch.ToString());
}
}
return operandStack.Pop();
}
/// Validates the infix expression for correctness
///
/// Infix expression to be validated
/// True if expression is valid
private static void ValidateInfixExpression(ref string expression)
{
expression = expression.Replace(” “, string.Empty);
// Rule 1: ‘(‘ and ‘)’ pair
// Rule 2: Every two operands must have one operator in between
}
/// Checks if character is a listed operator or not
///
/// Charaxter to be tested
/// False if not otherwise True
private static bool IsOperator(char character)
{
if ((character == ‘+’) || (character == ‘-‘) || (character == ‘*’) || (character == ‘/’))
{
return true;
}
return false;
}
/// Checks if popped operator has same or higher precedence than Current operator
///
/// Popped operator
/// Current operator in the expression
/// True if equal or higher precedence
private static bool CheckSameOrHighPrecedence(char elementToTest, char checkAgainst)
{
bool flag = false;
switch (elementToTest)
{
case ‘/’:
case ‘*’:
flag = true;
break;
case ‘+’:
case ‘-‘:
if ((checkAgainst == ‘+’) || (checkAgainst == ‘-‘))
{
flag = true;
}
break;
default: // for any other popped element
flag = false;
break;
}
return flag;
}
private static string PrefixExpressionBuilder(Stack operandStack, char operatorChar)
{
string operand2 = operandStack.Pop();
string operand1 = operandStack.Pop();
string infixExpression = string.Format(“{0}{1}{2}”, operatorChar, operand1, operand2);
return infixExpression;
}
SPONSORED



Thanks, it was rather educative. I’ve pasted it into visual studio and everything works correct.
LikeLike
This algorithm is completely messed up how you can commute when you encounter an operand and an operator from operand stack.e.g. take expression ((5+2)*3) then it’s prefix form should be (*3+52) =21.
while this algorithm will give(*+352)=16
LikeLike
this algo will work correctly if “Each prefix expression is push back onto the operand stack as either a left or right operand for the next operator “.
LikeLike
I would love if you can explain by an example
LikeLike
I would love if you can explain by an example
LikeLike
I implemented this in java and worked OK and gave me *3+25!
LikeLiked by 1 person
Infix to Prefix (Conversion, Evaluation, C++ Code)
LikeLike
can you please explain me 3rd example of infix to prefix?? please
LikeLike
The algorithm seems to be wrong. The solution is generated in the operandstack. Now look at step 3 : You pop always the 2 operands from the top of the operandstack and push it back with an operator in prefix mode. How does this solution ever provide any operator to end up on the bottom of the operandstack – its just a simple a prefix swapping on the stack top to my eyes!
LikeLike
Operand Stack will have only operands and NOT operator(s) at any stage
LikeLike
Giving a case/example here, can be helpful
LikeLike